The Vibrations of a Barrel Tuned for Positive Compensation
(Updated 18th November 2015)

"The art of producing extreme rimfire accuracy is at its best when informed by science."

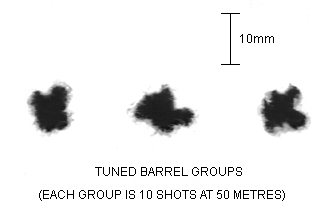
Introduction
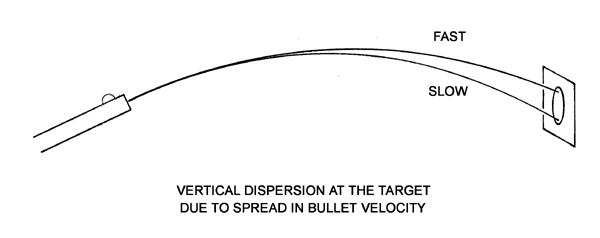
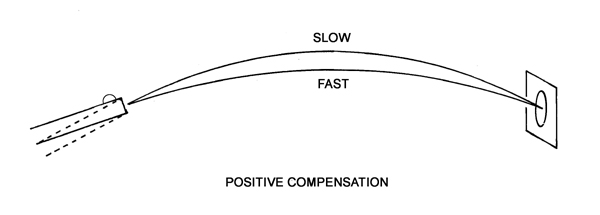
Mr A. Mallock ("Vibrations of Rifle Barrels", Proceedings of the Royal Society, Vol. 68, page 327, 1901) may not have been the first person to put forward the proposition that a rifle can be "tuned" to generate "positive compensation" at a given range, but it shows that this idea has been around for well over a century and is not a new one.

The proposition for positive compensation is based on the fact that when any given batch or type of ammunition is chronographed, there is a always a spread in muzzle velocity observed about a mean. As a consequence, there will be a vertical dispersion in the fall of shot at the target, as the slower bullets in the sample take longer to travel down the range and so drop further than the faster bullets. It is easy to compute what the vertical dispersion should be for a given batch of ammunition due to the observed spread in muzzle velocity.

Vertical dispersion due to velocity spread
Curiously though, it is also often - if not usually - observed that the calculated vertical dispersion is not evident on the target. To explain this observation, the concept of "positive compensation" is invoked. It is generally recognised that the shock of the recoil forces in the rifle generate transverse vibrations in the barrel. For positive compensation, it is envisaged that the bullet is exiting the muzzle during an upward swing in the vibration at the muzzle, such that faster bullets (which arrive at the muzzle slightly earlier than slow bullets) are launched at a slightly lower angle into their trajectory than slower bullets. This will tend to reduce the vertical dispersion in the group at the target resulting from the variation in muzzle velocity. And if the upward swing in the muzzle is exactly right, there will be complete positive compensation as the trajectories of bullets across the entire spread of muzzle velocities all meet at the same height on the target at a given range.

Positive compensation representation

If there is (almost) general agreement on the principle, the many attempts since Mallock's paper to be more quantitative about the actual vibrations on a rifle barrel, and how they may be controlled to produce positive compensation, have left us little further forward than we were a century ago. Some attacks of note are summarised below.

The earliest attempt of note to measure vibrations on a rifle barrel (a Model 71 Mauser) was that of Cranz and Koch (�Untersuchungen uber die Vibration des Gewehrlaufs.� Abhandlungen d. math-phys. C1 D. Akedemie Der Wissenachaften, Vol. 69, page 747-775, Munchen, 1899.) who used high-speed photography to follow the motion of a wire attached to various parts of the barrel.

In 1912, Francis Carnegie ("The Vibration of Rifle-Barrels", Min. of Proc. of Inst. of Civ. Eng., Vol. 191, page 217-255, 1912-13 Pt. 1) built on the work of earlier experimenters (cited therein) in using a camera focused on a back-lit pin-hole which had been drilled in a thin sheet of metal attached to the barrel of the rifle. The vertical excursions of the barrel were thus recorded as the rifle recoiled to give the time-base on the photographic plate. Their test subject was the S.M.L.E. .303 service rifle, both stocked and de-stocked. They achieved some good results - notwithstanding the variable nature of the time-base of data obtained in this way, and that the fact that the barrel did vibrate before the bullet exited the barrel was firmly established.

Following on from Carnegie's work, a very determined effort was made to study the dynamics of a rifle under recoil at Woolwich Arsenal during the early 1920s. This work was finally published as an internal report. ("On Rifle Barrel Vibrations and their Effect on the Angle of Jump", R.D. Report No. 63, 1925) They also used the S.M.L.E. rifle as their test subject and showed how careful experimental methods can yield very useful results even when using comparatively primitive methods. In fact, it would be a long time before their results were bettered. This report was only de-classified in 1959.

In 1927, Captain Philip P. Quale used an oscillograph* for his attempt to measure the vibrations on the barrel of a 1903 Springfield ("The Vibrations of Rifle Barrels", American Rifleman, January 1, page 17-32, 1927).
(*An immediate predecessor to the cathode ray oscilloscope, but using a high speed drum camera to record the movements of a beam of light bouncing off a small mirror, which was attached to a coil suspended between two powerful magnets.)

A decade later, A.E. Martin and J. Muir ("Vibrations of a Rifle Barrel", Journal of the Royal Technical College Glasgow, Vol. 4, Part 2, page 213-239, 1938) used a cathode ray oscilloscope (a novel instrument in 1938) to measure the excursions of a phonograph needle, placed on the muzzle of a Lee-Enfield .303 rifle. They compared their results to the resonant frequencies of transverse waves on a uniform steel bar of similar dimensions to the rifle barrel, with results that were suggestive at best. The dynamic behaviour of a rifle barrel responding to a complex, impulsive, bending moment at one end, was (and is) not tractable in an analytic form and the computing power to tackle the problem numerically would not be available for another thirty years.

Harold Vaughn ("Rifle Accuracy Facts", Pub. Precision Shooting Inc. Connecticut, 1998) took another tilt at the problem. For his experimental work, Vaughn used an accelerometer on the muzzle of the barrel. The resulting trace of acceleration with time had to be integrated - once to obtain the vertical velocity of the muzzle, and again to get at the position with time. These results were of limited use by themselves. The main value of Vaughn's experimental results was to check his theoretical computer model, which used a numerical "lumped parameter" approach to model the rifle barrel vibrations. The results were more convincing than those of Martin and Muir, sixty years before, but it was clear that Vaughn's computer model was not reproducing the dynamics of the rifle barrel with sufficient accuracy to be useful in the problem of achieving positive compensation by design.

The increasingly powerful computers of modern times has enabled various interested individuals to run highly sophisticated Finite Element Analysis (FEA) computer simulations of rifle barrel dynamics as the bullet is travelling up the barrel. Probably the most sophisticated computer simulation to date is that run by Al Harral using the LS-Dyna FEA code. This code was developed at Lawrence Livermore National Laboratories, where Al Harral worked using the LS-Dyna code to analyse mechanical structures. Al Harral realised the potential of harnessing the muzzle vibrations to achieve positive compensation at a given range and has attempted to design barrels specifically contoured to give the desired result. His work has lacked the experimental confirmation needed to verify his computer modelling, however.

Also notable amongst these campaigns using FEA modelling of rifle barrels is that of Kevin N. Schwinkendorf and Steven P. Roblyer ("Simulation of the Vibrational Response of a Rifle Barrel During Firing", Proceedings of the Advanced Simulation Technologies Conference, organized by the Society for Computer Simulation, page 66, April 5-9, 1998). It was the belief of these two authors that if the muzzle vibration could be "tuned", so that if the rate of change of muzzle angle was minimised (zero) at the time of bullet exit, the vertical dispersion of the group at the target due to the variation in muzzle velocity would be minimised. This assumption is only justified if the launch time of the bullet with reference to the vibration cycling on the barrel does not change with muzzle velocity. They ran simulations for various muzzle weights to tune the vibrations for a null at the bullet exit time. Practical tests were to follow to verify the simulation, but to my knowledge no results of any such tests have been published.

The influential American rimfire gunsmith Bill Calfee, in an article written for Precision Shooting Magazine ("I'm Feeling Those Good Vibrations AGAIN!" Vol. 52, No. 11, March 2005) presented a rather novel view on how barrels vibrate, and also expressed his belief that for best accuracy, barrels should be tuned so that the muzzle is "stopped" and there is no change in muzzle angle, or position, as the bullet is launched. It should be noted that Calfee's theories have absolutely no basis in fact and are mathematically untenable. But that does not stop it being the most quoted work in the popular press on barrel vibrations and the tuning of barrels.

Despite the increasing sophistication of the attack on the theoretical modelling of rifle barrel vibrations in recent years, experimental work of comparable accuracy to check the computer models has been notable in its absence. The work presented here is an attempt to start redressing the balance between experiment and theory so that future theoretical work can be better informed.

The apparatus
It is clear that the variable that is required to be measured is the angle of the muzzle of the barrel to the horizontal, and the way this varies with time as the bullet exits the barrel. All the experimental attempts listed above have measured the position, velocity, or acceleration of a point on the rifle barrel. The best these results could hope to do was inform a theoretical model which could calculate the rate of change of angle at the muzzle, but which could also generate data on the predicted position, velocity and acceleration at any point on the barrel with time with which the experimental results could be compared. It would be helpful to have experimental results that could stand alone as a useful tool in determining the optimum vibrations for positive compensation, rather than be a test of a theoretical model which would be depended on to generate the useful information.

Using a mirror attached to the muzzle in some way, so as to reflect a beam of light, is an obvious route. The excursions of the reflected beam would be a direct function of the vibrations of the barrel at the mirror, and could be measured in a number of ways. However, such an apparatus would be difficult to set up and very cumbersome, as its sensitivity would proportional to its size and the angular variation expected is small.

The method finally chosen was to attach a thin sheet of polarising plastic to the muzzle. Beams of light would be shone through the polarising sheet onto polarised detectors. If the planes of polarisation of the polarising plastic sheet and the polarised detectors were set at 45 degrees, the change in signal in the detectors would be proportional to the change in angle of the polarising sheet - and so the muzzle of the barrel. By using two detectors polarised at 90 degrees to each other and combining the two signals in a differential amplifier, the signal would also be insensitive to any common-mode changes such as in the intensity of the light sources.

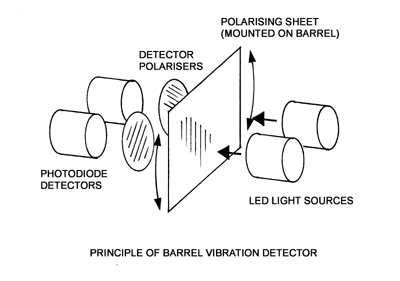Principle of apparatus

Such an apparatus could be compact, sensitive, easy to set up, and would have the added benefit that it would only be sensitive to changes in angle of the polarising plastic sheet about an axis perpendicular to the plane of the sheet. It would not be sensitive to any other degree of freedom such as a change in position either up-down, backwards-forwards or sideways or rotation about any other orthogonal axis.

Experimental setup

A "muzzle gate" was also required to detect the exact moment the bullet exited the barrel. This was a simple photoelectric device, using photodiodes to detect the interruption of light from an LED array as the bullet passed between them. The experimental setup is shown above. The polarising sheet is attached temporarily to the bottom of the barrel using "Blu-Tac", a malleable plastic adhesive. The bottom of the sheet is seen sitting in the slot of the sensor head, which contains the light sources, the polarised detectors and the first stages of the differential amplifier. The muzzle gate is seen sitting in front of the muzzle of the barrel. A contact microphone is attached to the action using a magnet and this detects the sound of the firing pin hitting the case. This signal is used to trigger the digital oscilloscope used to record the signals from the sensor head and the muzzle gate.

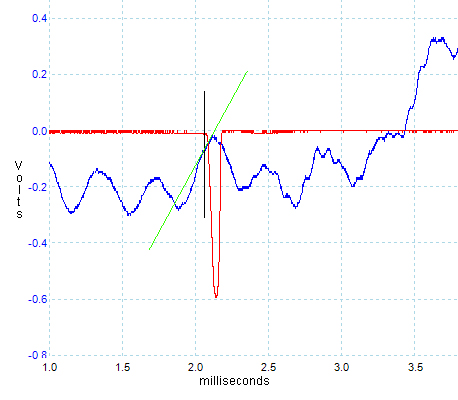
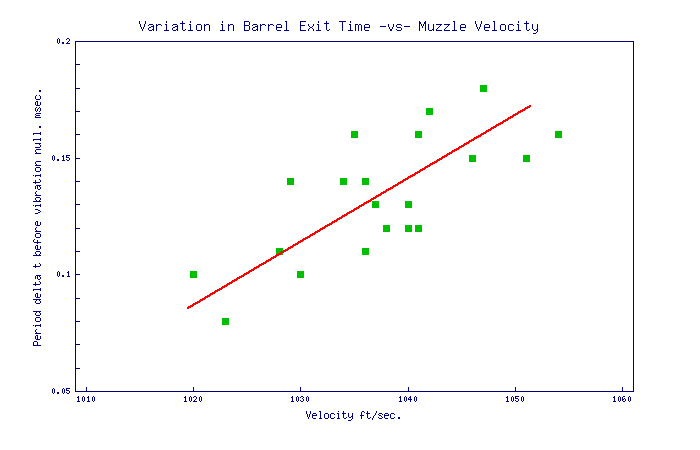
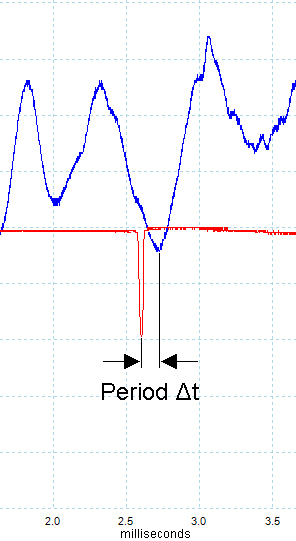
Exit time variationVariation of muzzle velocity with bullet exit time
The first step in deducing what rate of change of angle at the muzzle is required to give positive compensation, is to know how the exit time of the bullet at the muzzle varies with muzzle velocity.

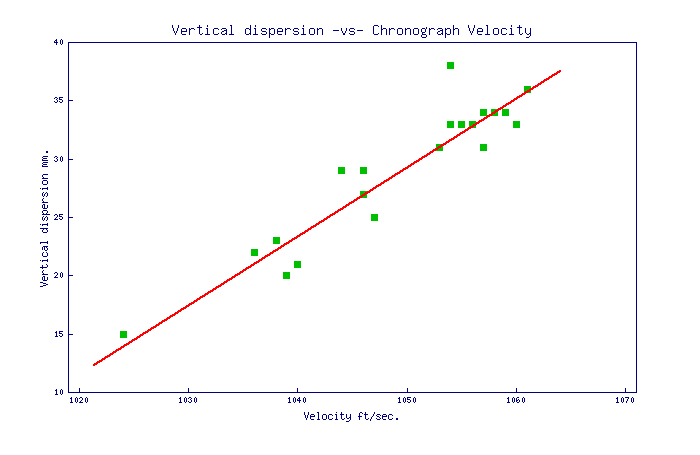
For this experiment, the muzzle velocity was determined using an Ohler 35 chronograph. The two sky screens were separated by four feet and they were centred on a point five feet ahead of the muzzle. The absolute value of the muzzle velocity was not too critical for this experiment as it was the differences in muzzle velocity that were of interest. Because of this, it was important that the 'jitter' on the measured muzzle velocity was minimised. In an attempt to minimise the jitter of the chronograph, an LED array forming a 'light bar' 6 inches long and of width 0.08", was placed 8 inches above each sky screen. This formed a thin light source above each sky screen of uniform and constant brightness along its length.

To measure the variation in bullet exit time from the muzzle, it would seem obvious to measure the variation in the interval between the contact microphone trigger signal (ie when the firing pin struck the case) and the bullet passing through the muzzle gate. But it was expected that there would be some variation in the initiation in burning of the primer and powder after the fall of the firing pin. This variation could mask the looked for variation in bullet exit time, due to variation in muzzle velocity, to some significant extent. However, it is the pressures generated by the burning primer and powder that gives rise to the barrel vibrations. While variations in the pressures may alter the amplitude of the vibrations, it was considered that the time history of the barrel vibrations would remain constant as this would be due to the mechanical structure of the rifle itself, and this would not change from shot to shot. The best way to measure the variation in bullet exit time would be with reference to the barrel vibrations, rather than the trigger signal.

The trace on the right shows a portion of signal indicating the changing muzzle angle (blue) around the time when the bullet exited the muzzle, as indicated by the momentary downward 'blip' in the muzzle gate signal (red). The period 'delta t' from the muzzle gate signal to the following null in vibration signal was measured for each shot fired, along with the measured velocity.

The graph below shows the results for Eley EPS Tenex ammunition. The data are rather noisy, but there is a fairly clear trend that for a change in muzzle velocity of 375 ft/sec., the exit time is changing by 1 millisecond. The barrel in this case was 26 inches long. This is expected to be a fairly universal constant applicable to all rimfire barrels of this length, shooting subsonic target ammunition.

Indeed, it may be that this is a universal constant for rimfire barrels of any length over six inches (approximately), after which friction is increasingly the dominant force on the bullet during its travel up the barrel. Thus, it can be argued that to first order, the spread in velocity of the bullets in the barrel will increase linearly with distance travelled up the barrel past the six inch point, and the rate of change of barrel travel time with velocity will remain fairly constant with length.

Variation in bullet exit time -vs- muzzle velocity

Variation in launch angle with muzzle velocity required for complete positive compensation at 50 metres
Using the Trajectory program, it is trivial matter to compute the change in muzzle angle required for complete positive compensation at 50 metres, for a given range of muzzle velocity. So, for a velocity of 1010 ft/sec. the launch angle needed is 9.3 MOA and for 1060 ft/sec. the required launch angle is 8.5 MOA to hit the target at the same height.

The rate at which the angle of the muzzle has to change with muzzle velocity, so all the shots hit the target at the same height and there is complete positive compensation, is 0.016 MOA for 1 ft/sec. change in muzzle velocity.

Rate of change of muzzle angle required for complete positive compensation at 50 metres
Multiplying together the Variation of muzzle velocity with bullet exit time and the Variation in launch angle with muzzle velocity required for complete positive compensation at 50 metres, the required rate of change of muzzle angle with time is 6.0 MOA per millisecond for a 26 inch barrel.

A case study
A barrelled action was placed in the Border Barrels test rig. (See the picture to the right). The barrel length was 26" and the diameter was 0.943". However, it was protruding only 17 inches in front of the barrel clamp, by which the barrelled action was attached to the rig. (Note that this rig was not rigid. The relatively thin base plate flexed under recoil and allowed the barrel clamp to rotate backwards, resulting in an upwards vertical muzzle flip.) Experience had shown that with such a short length of barrel ahead of the clamp, the groups with a bare barrel would be strung vertically. (The photo shows the barrel with a 200 gram weight clamped on it at the muzzle.) This barrel was no exception. It is clear from the three groups in the photo below that at 50 metres, using Eley EPS Tenex, the shots were stringing vertically.

Bare barrel groups

Test case barrel
Bare barrel vertical dispersion at the target

The graph above is a plot of the height of a number of shots above a randomly drawn line on the target, as a function of muzzle velocity. The red line is a fit through the data and has a slope showing a drop in height on the target of 0.595mm for each ft/sec. decrease in muzzle velocity. This is equivalent to 0.041 MOA for each ft/sec. decrease in muzzle velocity.

But there will naturally be a drop at the target of 0.016 MOA for every ft/sec. drop in muzzle velocity, just because the bullet takes a little longer to get there (see above). So it is assumed that the remaining 0.025 MOA for every ft/sec. change in muzzle velocity will be due to a change in the muzzle angle at bullet launch. It was shown above that the muzzle velocity varies with the exit time of the bullet at the muzzle at 375 ft/sec. per millisecond. As the bullets were exiting the muzzle of the bare barrel then, the muzzle must have been swinging downwards at a rate of 9.4 MOA per millisecond (0.025 MOA per ft/sec. multiplied by 375 ft/sec. per millisecond) to produce the observed vertical dispersion at the target.

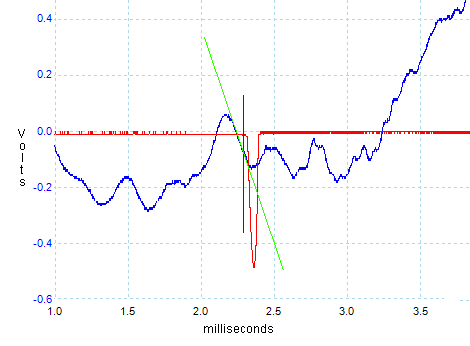Vibration of bare barrelThe image to the right is a trace of the rate of change of angle at the muzzle of the bare barrel, as taken using the apparatus described above. The blue trace is the angle of the muzzle. The vertical axis is in volts. The calibration determined during testing of the apparatus on the bench was that 0.16 volts is equivalent to 1 MOA. The red trace is the muzzle gate and the negative blip show when the bullet passed through the muzzle gate. But the muzzle gate was about one inch in front of the muzzle, so the actual moment when the bullet was exiting the muzzle would have been about 0.1 milliseconds earlier, where the black vertical line has been placed.

The green line set against the muzzle angle trace at the moment the bullet was exiting the barrel shows the rate at which the muzzle angle was changing at that time. The rate was -9.4 MOA per millisecond. This is in perfect agreement with the rate calculated from the vertical dispersion at the target above. The difference is that only one shot was required to determine this rate of change of muzzle angle using the apparatus described, whereas twenty shots were needed to determine it from the fall of shot on the target.

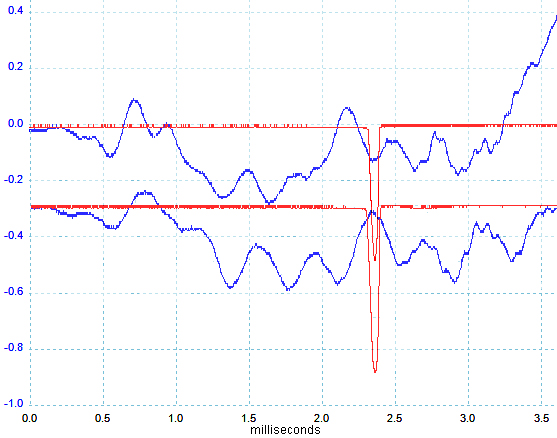Vibrations with and without tuner In the image on the right, the top trace is the barrel vibrations from the bare barrel, discussed above, and the bottom trace is the barrel which has now been "tuned" with a 200 gram weight attached to the front of the barrel. The traces have been superimposed so that the bullet exits appear at same time. As can be seen, the general shape or pattern of vibrations for the two traces is very similar. However, while the vibrations on the two traces start out in a very similar way, the pattern of vibrations with the weighted barrel appears slightly stretched in time compared to that of the unweighted barrel.
Looking at the vibration trace of the "tuned" barrel in more detail, the vertical black line once again shows the moment the bullet was exiting the barrel. The green line laid against the trace for that moment shows the rate at which the barrel was swinging upward in angle as the bullet exited barrel. The rate is 6.0 MOA per millisecond. This will be recognized from the discussion above as the exact rate required to give complete positive compensation at 50 metres.

In theory, this barrel with a 200 gram weight on the front should have perfect positive compensation at 50 metres. So, how did it shoot?

See the groups below.

Groups with tuner

The groups are self evidently 'round', the spread now being primarily caused by dispersive forces due to factors such as the off-axis centre of gravity in the bullets, and the bullets being upset on launch due to the wash of the muzzle blast over their base. Unlike the dispersion caused due to variation in muzzle velocity, these forces have no preferred axis in which they act and so result in round groups. It is the roundness of the groups, being as wide as they are tall, (subject to the usual statistical uncertainties), which shows that vertical dispersion is no longer a significant factor.

 Tuned barrel

Conclusions
It has been shown that the launch time of the bullet from the barrel, with reference to the transverse vibrations in the barrel, does vary with muzzle velocity, and this rate has been measured for Eley Tenex .22 rimfire ammunition in a 26 inch barrel. The proposition that positive compensation might be achieved by "tuning" a barrel, such that the muzzle angle is changing with time in a beneficial way at bullet launch, is thus a valid one.

In a test case, the vertical dispersion at a range of 50 metres was measured as a function of muzzle velocity for an "untuned" barrel. From this dispersion, and the known rate of change of launch time with muzzle velocity for a 26 inch barrel, a rate of change of angle at the muzzle for this barrel was calculated. Using an apparatus built to measure the rate of change of angle of a barrel, the rate of change of angle at the muzzle was measured and this agreed with that calculated from the group dispersion. This demonstrated that the apparatus was working as designed. It also showed that the vertical velocity of the muzzle is probably not significant in contributing to the vertical dispersion of the group in general, compared to the rate of change of muzzle angle, and was certainly not so in this case.

Finally, the barrel was "tuned" by attaching a weight to the front of the barrel, such that the rate of change of angle at the muzzle was now 6.0 MOA per millisecond at bullet launch, which is the rate of change required for complete positive compensation at 50 metres. The groups fired with the tuned barrel were small and round, showing no sign of vertical dispersion, so demonstrating that positive compensation had been achieved.

The measurement of barrel vibrations in the way demonstrated will be a very quick and positive method of tuning a rifle, requiring very few shots and very little time. Moreover, there is no ambiguity or uncertainty about the result. When the barrel is tuned for complete positive compensation, no further improvement is possible.